Anderson mixing (AM) (Anderson, 1965) is a classical method that can accelerate fixed-point iterations by exploring the historical information stored in \(m\) vector pairs, where \(m\) is called memory size. AM has been widely used in scientific computing and has achieved great success for solving fixed-point problems. Since many optimization problems can be casted as fixed-point problems, AM can also be used in optimization.
Although AM is empirically superior than gradient descent method, there are several issues of applying AM to solve large-scale and high-dimensional optimization problems in a resource-limited machine:
- The superiority of AM in terms of convergence rate has not been justified;
- The memory cost of AM can be prohibitive;
- AM is unaware of the symmetry of Hessian matrices in optimization problems, and the approximate Hessian matrix of AM is generally not symmetric.
In our recent NeurIPS 2022 paper, we address the aforementioned issues of AM by developing a variant of AM with minimal memory size (Min-AM), where only one additional modified vector pair need to be stored, namely the memory size is 1. Min-AM forms symmetric Hessian approximations and has definitely improved convergence over gradient descent (GD) method. We validate the correctness of the theory and the practical performance of Min-AM by solving several deterministic optimization and stochastic optimization problems.
Anderson mixing
For solving optimization problems, Anderson mixing can be interpreted as a two-step procedure: (i) Projection step: Use the historical iterations to interpolate an intermediate iterate, where the interpolation coefficients are determined by a projection condition. (ii) Mixing step. Incorporate the current gradient into the intermediate iterate, where the step length is called mixing parameter.
It is proved that AM has locally linear convergence (Toth & Kelley, 2015), but the superiority of AM over GD is not well explained. Also, AM does not form symmetric approximations to Hessian matrices and has memory issue in practice.
Anderson mixing with minimal memory size
We propose a variant of AM with minimal memory size (Min-AM) to address the issues of the classical AM. Also, by using the properties of Min-AM, we can estimate the eigenvalues of the Hessian matrix via an economical eigenvalue estimation procedure. The eigenvalue estimates for the smallest and largest eigenvalues of the Hessian are used for adaptively choosing the mixing parameters.

The figure shows the exact eigenvalues of the Hessian and the eigenvalue estimates computed by Min-AM during iterations, for solving a strongly convex quadratic problem. We find that the exact smallest and the largest eigenvalues are well approximated after a small number of iterations.
The Min-AM methods consist of the basic Min-AM, the restarted Min-AM, and the stochastic Min-AM.
The basic Min-AM
The basic Min-AM stores a modified vector pair and introduces an additional projection step to the original update scheme of AM. It exploits the symmetry of the Hessian, and is essentially equivalent to conjugate gradient (CG) method and the full-memory Type-I AM (AM-I) in strongly convex quadratic optimization.
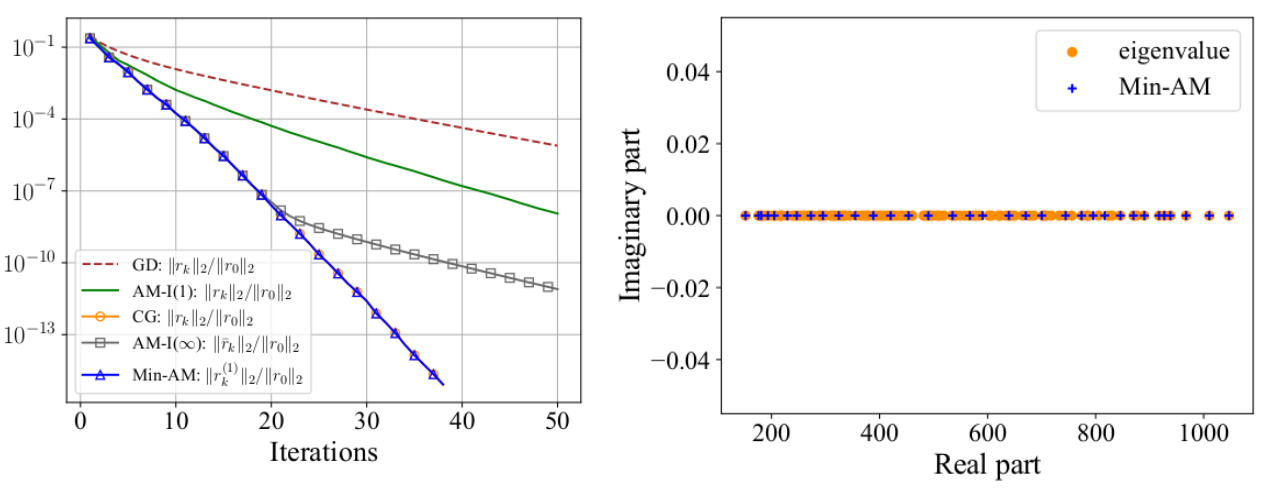
The numerical results conform to our theorem of the basic Min-AM. It also shows that Min-AM has better numerical stability than the full-memory AM-I.
The restarted Min-AM
For solving general nonlinear optimization problems, we introduce restarting conditions to the basic Min-AM and obtain the restarted Min-AM. The restarted Min-AM has definitely better convergence than GD in theory.
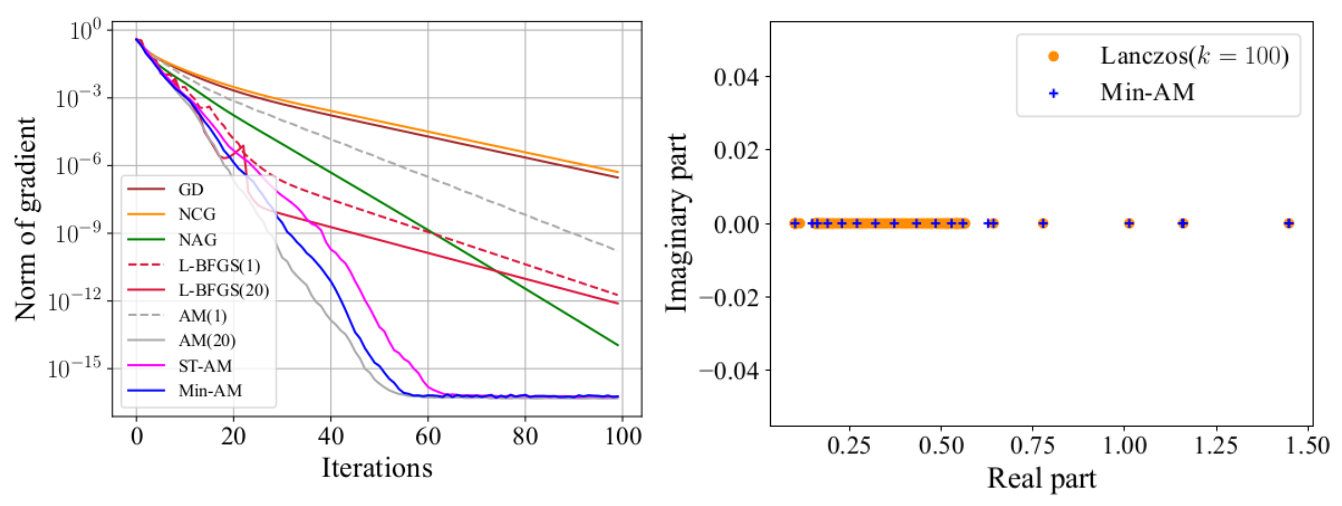
The tests of regularized logistic regression demonstrate the fast convergence of Min-AM. The figure shows the results on the madelon dataset. We find the restarted Min-AM is competitive and the eigenvalue estimates also roughly match the Ritz values computed by Lanczos algorithm (Ritz values can approximate the true eigenvalues).
The stochastic Min-AM
To solve stochastic optimization, we introduce regularization and damping techniques to the basic Min-AM and obtain the stochastic Min-AM (sMin-AM) that has convergence guarantee in nonconvex stochastic optimization. We prove that sMin-AM can achieve the asymptotically optimal iteration complexity of the black-box stochastic first-order methods.
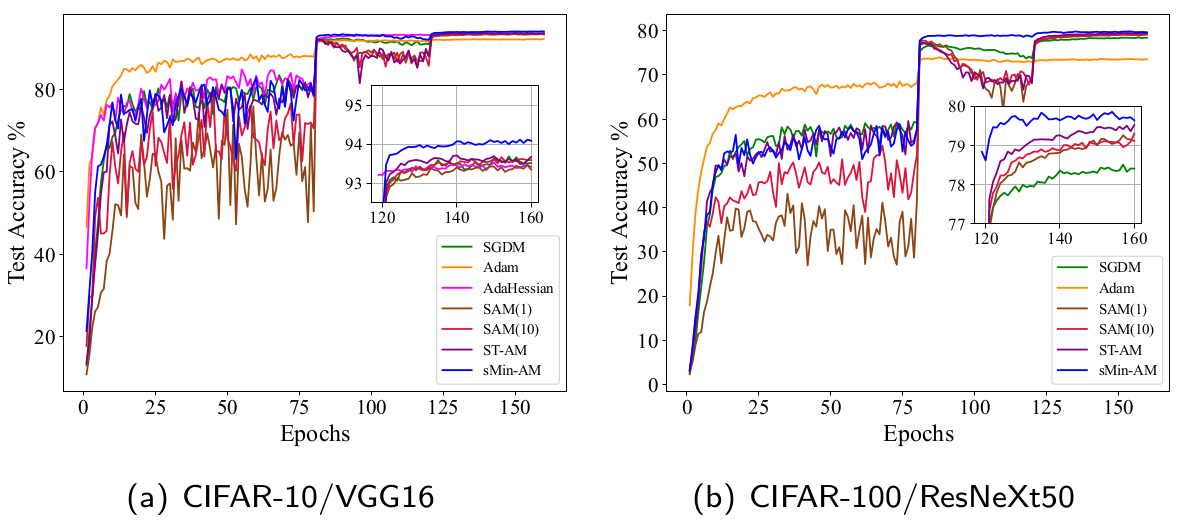
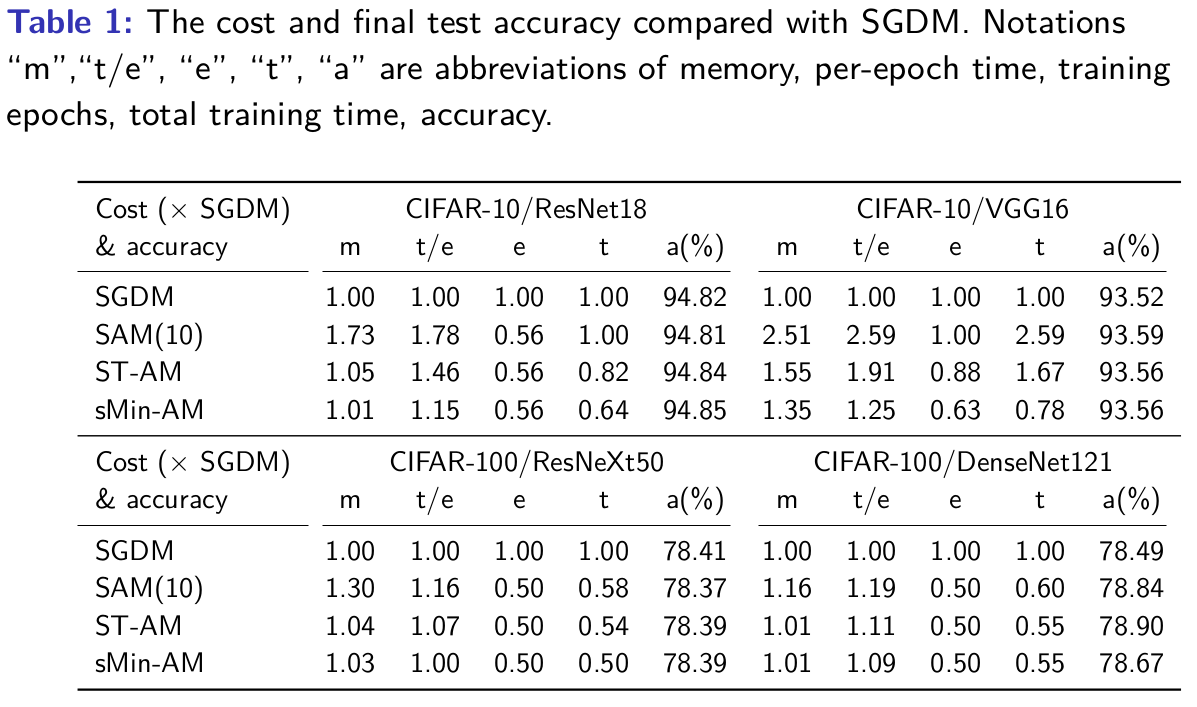
The numerical results of training neural networks on CIFAR-10 and CIFAR-100 demonstrate that the sMin-AM outperforms SGDM and Adam while being more memory-efficient than stochastic AM (SAM) (Wei et al., 2021) and short-term recurrence AM (ST-AM) (Wei et al., 2022).
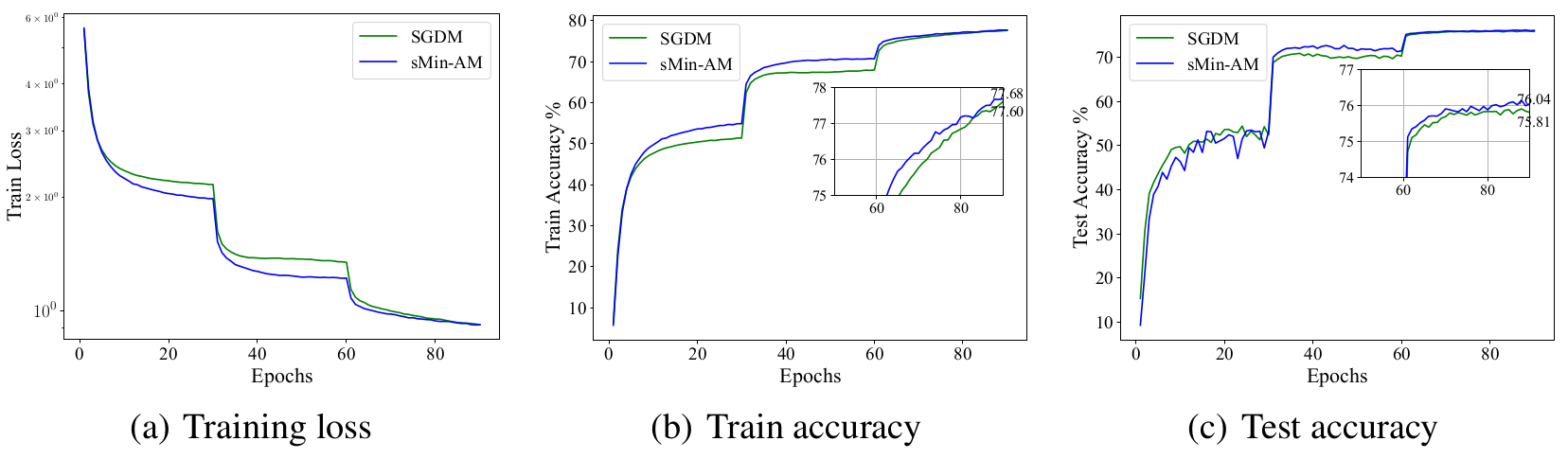
sMin-AM also performs well when training ResNet50 on ImageNet. It can be found that sMin-AM has faster training process and attains higher training accuracy and test accuracy than SGDM. For more, check out our NeurIPS 2022 paper =)
- Also see the previous blogposts in this series! – A Class of Short-term Recurrence Anderson Mixing Methods and Their Applications – Stochastic Anderson Mixing for Nonconvex Stochastic Optimization
Conclusion
We develop a variant of Anderson mixing with minimal memory size (Min-AM) for solving optimization problems. Min-AM exploits the symmetric of the Hessian. It achieves the minimal memory size and forms symmetric Hessian approximations. We prove the definitely better convergence rate of Min-AM than gradient descent method for solving nonlinear optimization problems, and also propose a strategy that adaptive chooses the mixing parameter based on an economical eigenvalue estimation procedure. We also give an extension of Min-AM for solving stochastic optimization. The experimental results in deterministic optimization and stochastic optimization demonstrate the efficiency of our proposed methods.
Contact
For further discussion, please contact: Fuchao Wei (wfc16@mails.tsinghua.edu.cn).
References
Donald G Anderson. Iterative procedures for nonlinear integral equations. Journal of the ACM (JACM), 12(4):547–560, 1965.
Alex Toth and C. T. Kelley. Convergence analysis for Anderson acceleration. SIAM Journal on Numerical Analysis, 53(2):805–819, 2015.
Fuchao Wei, Chenglong Bao, and Yang Liu. Stochastic Anderson mixing for nonconvex stochastic optimization. Advances in Neural Information Processing Systems, 34, 2021.
Fuchao Wei, Chenglong Bao, and Yang Liu. A class of short-term recurrence Anderson mixing methods and their applications. In International Conference on Learning Representations, 2022.
