Stochastic optimization is important in various areas such as statistics, machine learning and power systems. The concerned problem can be formulated as \(\min_{x \in \mathbb{R}^d} f(x)=\mathbb{E}_{\xi}\left[ F(x;\xi) \right]\), where \(F: \mathbb{R}^d \times \Xi \rightarrow \mathbb{R}\) is continuously differentiable and possibly nonconvex and the random variable \(\xi \in \Xi\) may follow an unknown probability distribution. It is assumed that only noisy information about the gradient of \(f\) is available through calls to some stochastic first-order oracle (\(SFO\)). The sampled average is the empirical risk minimization: \(\min_{x \in \mathbb{R}^d} f (x) = \frac{1}{T}\sum_{i=1}^{T}f_{\xi_i}(x)\), where \(f_{\xi_i}: \mathbb{R}^d \rightarrow \mathbb{R}\) is the loss function corresponding to the \(i\)-th data sample and \(T\) denotes the number of data samples. \(T\) can be extremely large such that it prohibits the computation of the full gradient \(\nabla f\).
One classical method is the stochastic approximation (also known as stochastic gradient descent (SGD)) [1] , which uses the negative stochastic gradient as the searching direction. Many algorithms were developed to accelerate SGD, such as the adaptive learning rate methods including Adagrad [2] and Adam [3]. In practice, the choices of optimizers can vary for different applications and their practical performances are still unsatisfactory in terms of convergence rate or generalization.
In our recent NeurIPS 2021 paper, we develop a novel second-order method based on Anderson mixing (AM) [4]. Our analysis and experiments show the proposed method is competent from both theoretical and practical perspectives and performs well in training various neural networks in different tasks.
Anderson mixing
Anderson mixing (AM) is a sequence acceleration method in scientific computing. It is used to accelerate the slow convergence of nonlinear fixed-point iterations. By using several historical iterations, AM aims to extrapolate a new iterate that satisfies certain optimality property. When the function evaluation is costly, the reduction of the number of iterations brought by AM can save large amount of computation. AM turns out to be closely related to multisecant quasi-Newton methods in nonlinear problems or the GMRES method in linear problems. Since gradient descent with constant stepsize can be viewed as a fixed-point iteration, applying AM to accelerate gradient descent method is a natural idea.

The figure shows the trajectories of using the Heavy-ball method, Adam, and AM to minimize a high-degree polynomial function of two variables. It is found that AM can arrive at the global minimum \((3,0.5)\) much faster than the other two optimizers.
Although AM performs well in practice, only local linear convergence of AM for fixed-point iterations has been proved, and there exists no version of AM that guarantees convergence for nonconvex optimization, let alone stochastic optimization. In this work, we introduce stochastic Anderson mixing to address these problems.
Stochastic Anderson mixing
We first reformulate Anderson mixing as a two-step procedure: (i) Projection step. The historical iterations are used to interpolate an intermediate iterate by solving least squares problem. (ii) Mixing step. The current gradient is incorporated to the intermediate iterate. To obtain a global convergent version of AM, we introduce damped projection and adaptive regularization to the original AM:
(1) Damped projection. Motivated by damped Newton’s method, we introduce damping to stabilize the projection step.
(2) Adaptive regularization. The step size calculated by the projection step may be too large, which leads to the overshooting problem. We introduce an adaptive regularization term in the projection step as rectification.
The resulting algorithm is the stochastic Anderson mixing (SAM). We also provide a procedure to ensure the current searching direction is a descent direction.
With these modification, we establish the convergence theory of SAM, including the almost sure convergence to stationary points and the worst-case iteration complexity. Moreover, the complexity bound can be improved to \(O(1/\epsilon^{2})\) when randomly choosing an iterate as the output.
Enhancement of Anderson mixing
We introduce two techniques to further enhance SAM:
(1) Variance reduction. By borrowing the stochastic variance reduced gradient technique, the iteration complexity of SAM is reduced to \(O(1/\epsilon)\).
(2) Preconditioned mixing. Motivated by the great success of preconditioning in scientific computing, we present a preconditioned version of SAM, where the simple mixing step of the original AM is replaced by a preconditioned mixing. The preconditioning can be implicitly done with any optimizer at hand.
Applications in training neural networks
We apply the new method and its enhanced version to train neural networks.
MNIST

For training a simple convolutional neural network (CNN) on MNIST dataset with large batch sizes, our method (AdaSAM) achieves significant acceleration.

The variance reduced extension (AdaSAM-VR) can achieve a lower training loss.

The preconditioned versions (RMSprop-AdaSAM and Adagrad-AdaSAM) also converge faster to an acceptable loss.
CIFAR
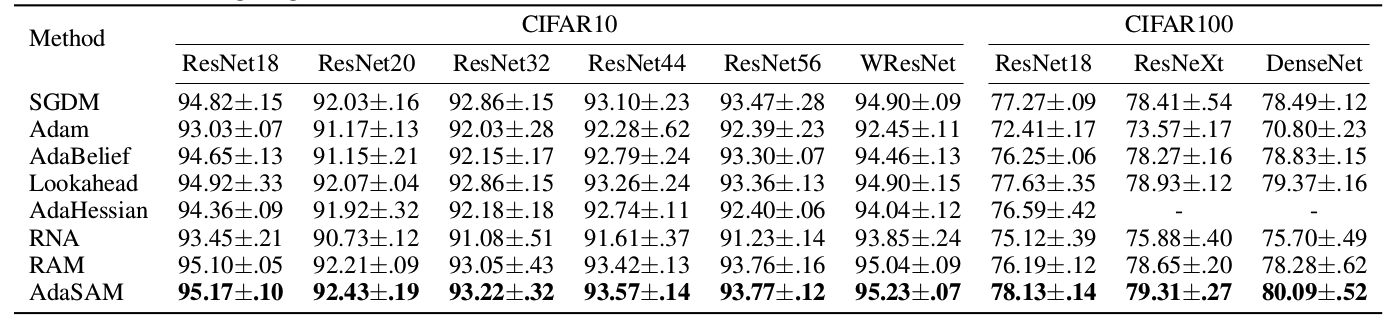
We trained ResNet, WideResNet (abbreviated as WResNet), ResNeXt, and DenseNet on CIFAR10 and CIFAR100. The results demonstrate the superiority of our method.
PTB

We also applied our method to training a 3-layer LSTM on PTB. The results show that our method (pAdaSAM) also outperforms other optimizers.
Conclusion
We develop an extension of Anderson mixing, namely Stochastic Anderson Mixing (SAM), for nonconvex stochastic optimization. By introducing damped projection and adaptive regularization, we establish the convergence and complexity analysis of our new method. To further improve convergence or test performance, we enhance the basic method SAM with variance reduction and adaptive regularization. Experiments show encouraging results of our method and its enhanced versions in training different neural networks in different machine learning tasks. These results confirm the suitability of Anderson mixing for nonconvex stochastic optimization.
Contact
For further discussion, please contact: Fuchao Wei (wfc16@mails.tsinghua.edu.cn).
References
[1] Herbert Robbins and Sutton Monro. A stochastic approximation method. The annals of mathematical statistics, pages 400–407, 1951.
[2] John Duchi, Elad Hazan, and Yoram Singer. Adaptive subgradient methods for online learning and stochastic optimization. Journal of machine learning research, 12(7), 2011.
[3] Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
[4] Donald G Anderson. Iterative procedures for nonlinear integral equations. Journal of the ACM (JACM), 12(4):547–560, 1965.
