Anderson mixing (AM) (Anderson, 1965) is a powerful acceleration method for fixed-point iterations. It extrapolates each new iterate using historical iterations. It is known that Anderson mixing is essentially equivalent to GMRES for solving linear systems (Walker & Ni, 2011). In the nonlinear case, it is recognized as a multi-secant quasi-Newton method (Fang & Saad, 2009) and has local linear convergence (Toth & Kelley, 2015).
Anderson mixing has several advantages, such as no additional functional evaluations and fast convergence in practice. However, one of the major concerns is the memory issue. Since the limited-memory method AM(m) uses \(m\) historical iterations for extrapolation, the additional memory cost is \(2m\) vector pairs of dimension $d$. Such memory cost can be prohibitive for solving high-dimensional problems in a resource-limited machine.
In our recent ICLR 2022 paper, we address the memory issue by developing the short-term recurrence Anderson mixing (ST-AM) methods, where only two additional vector pairs need to be stored, namely \(m=2\). Our methods have the nature of quasi-Newton methods while the memory cost is largely reduced to be close to first-order methods. We validate the effectiveness of ST-AM in several applications including solving fixed-point problems and training neural networks.
Anderson mixing
We first interpret Anderson mixing as a two-step procedure: (i) Projection step. The historical iterations are used to interpolate an intermediate iterate by solving a least squares problem. (ii) Mixing step. The current gradient is incorporated into the intermediate iterate.
AM is widely used to accelerate the slow convergence of fixed-point iterations in scientific computing, e.g., the self-consistent field iterations in electronic structure computations, full-waveform inversion. It is often found that AM can largely reduce the number of iterations to convergence. However, the memory overhead is a critical issue that prohibits the application of AM to large-scale and high-dimensional problems.
Short-term recurrence Anderson mixing
We address the memory issue of AM by developing a class of short-term reccurence AM (ST-AM) methods. In the ST-AM methods, only two additional vector pairs need to be stored.
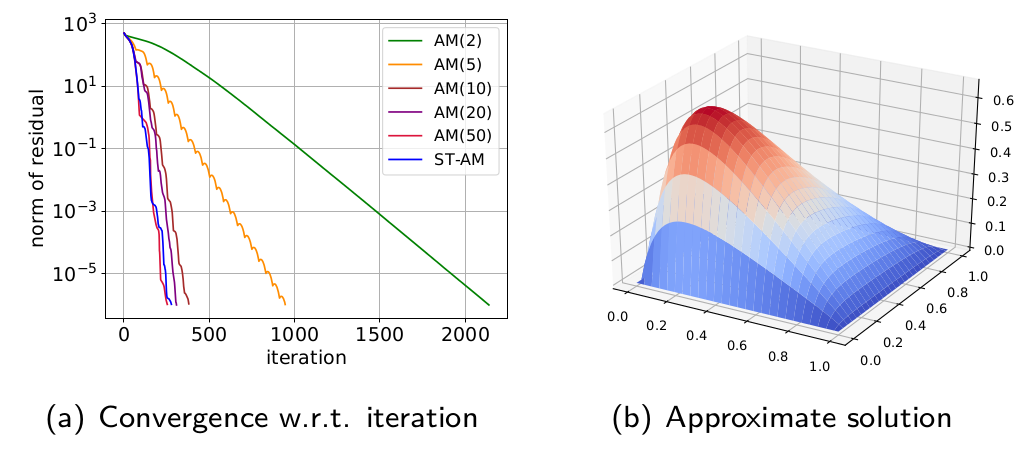
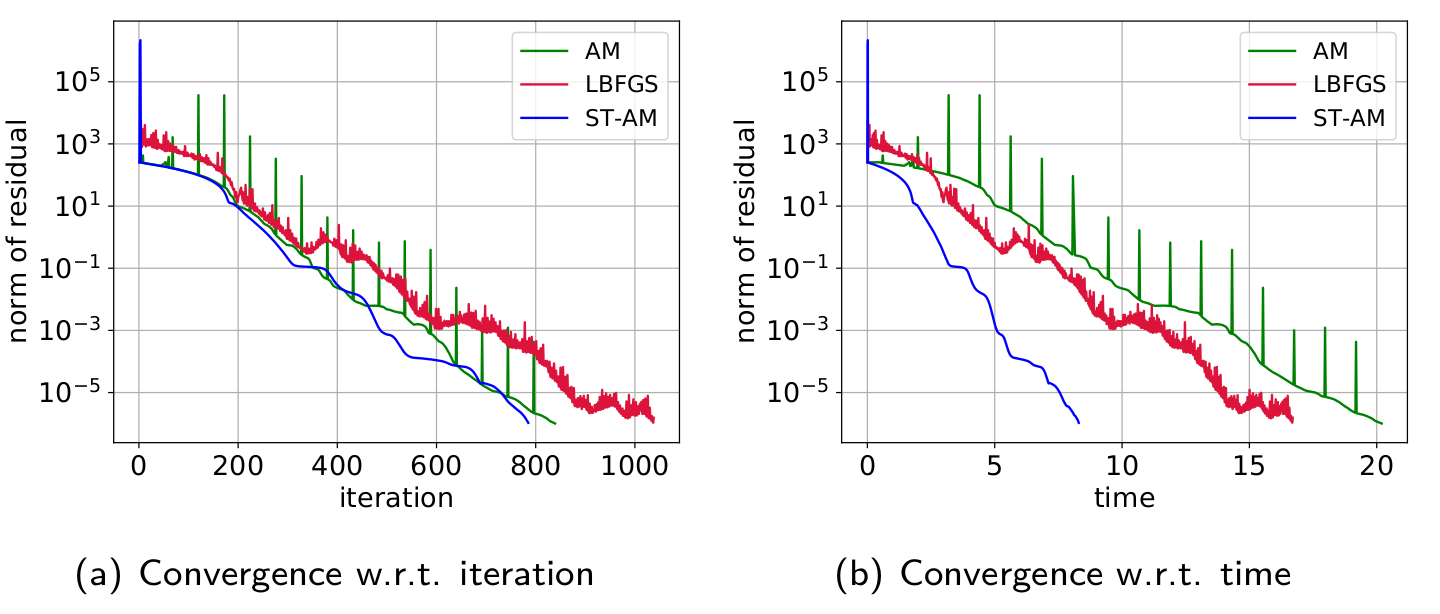
The figures show applying AM, LBFGS, and ST-AM to solve partial differential equations (PDE). The first one is the convection-diffusion problem and the second one is the Bratu problem. The convergence behaviours suggest that ST-AM is very efficient for solving the traditional PDE problems in scientific computing.
The ST-AM methods consist of the basic ST-AM, the modified ST-AM and the regularized ST-AM.
The basic ST-AM
By exploiting the symmetry of the Hessian in optimization, the basic ST-AM is equivalent to GMRES and the full-memory AM in strongly convex quadratic optimization. It also has linear convergence rate for solving nonsymmetric linear systems.
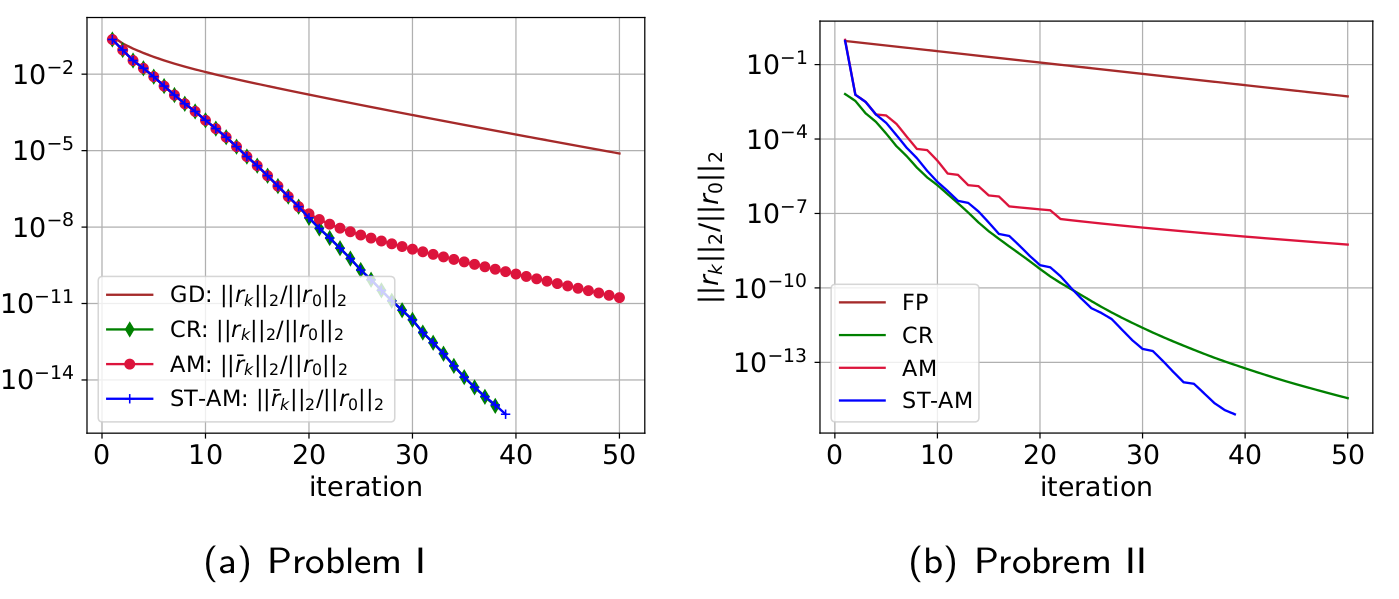
The numerical results conform to our theorems (Problem I: a strongly convex quadratic optimization; Problem II: a nonsymmetric linear system). It also shows that ST-AM has better numerical stability than the full-memory AM.
The modified ST-AM
For solving general nonlinear fixed-point problems, we introduce some minor changes to the basic ST-AM and obtain the modified version. The modified ST-AM (MST-AM) has improved local linear convergence.
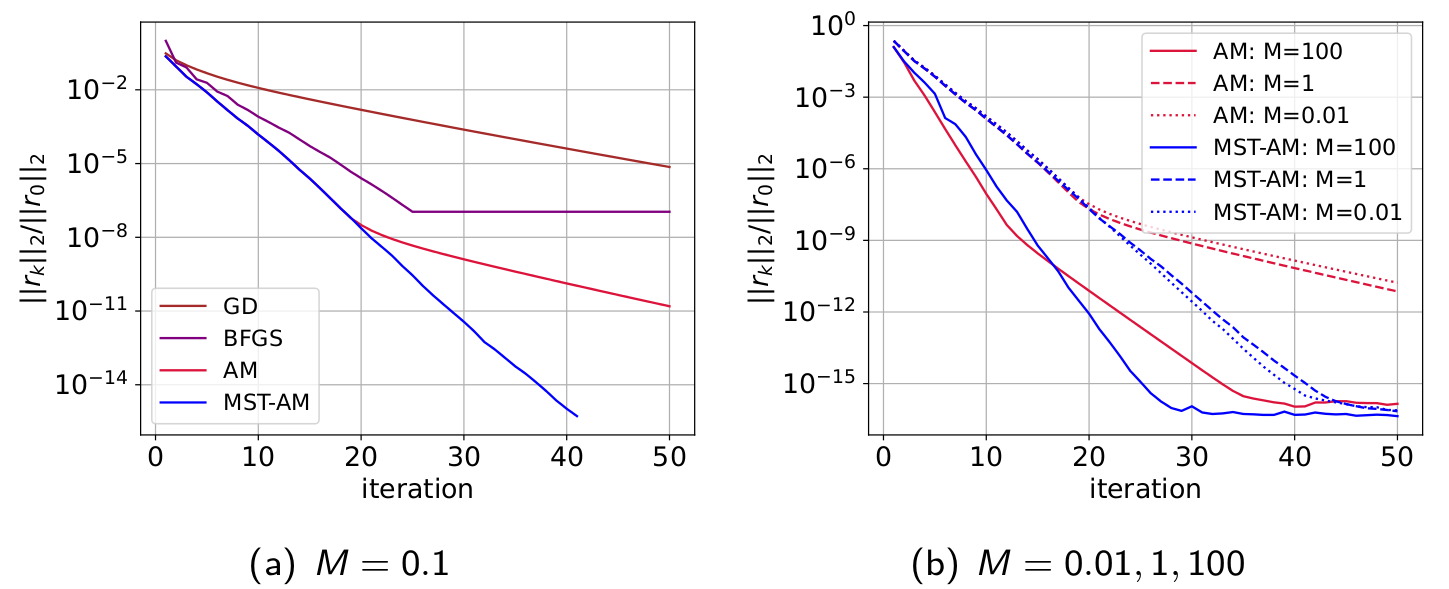
The tests about the cubic-regularized quadratic optimization demonstrate the fast convergence of MST-AM.
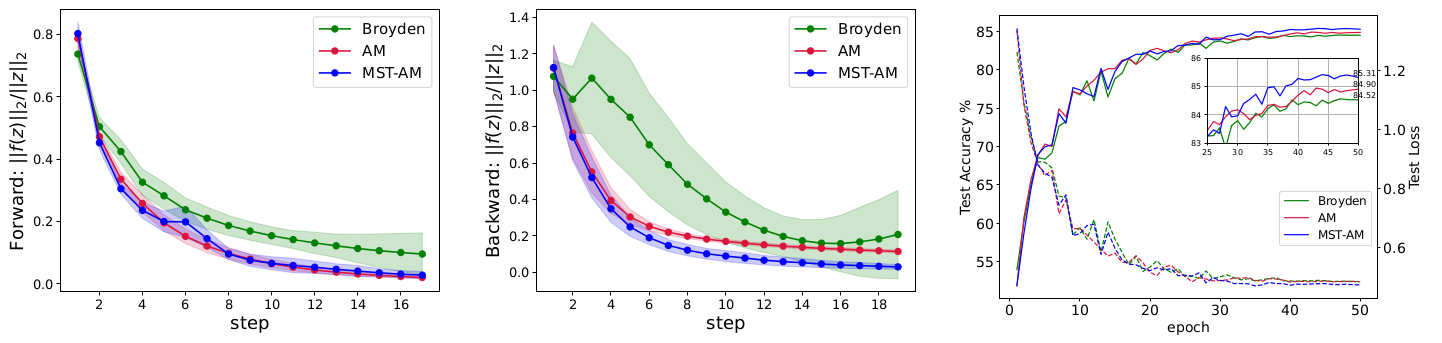
The MST-AM is also comparable to AM and the Broyden’s method for solving the root-finding problems in the multiscale deep equilibrium model.
The regularized ST-AM
To solve stochastic optimization, we introduce a regularized short-term recurrence form to the basic ST-AM. We also incorporate the damped projection and adaptive regularization techniques from stochastic Anderson mixing (SAM) (Wei et al., 2021) into ST-AM. The resulting method is the regularized ST-AM (RST-AM). RST-AM has global convergence for stochastic optimization, and the iteration complexity is \(O(1/\epsilon^2)\).
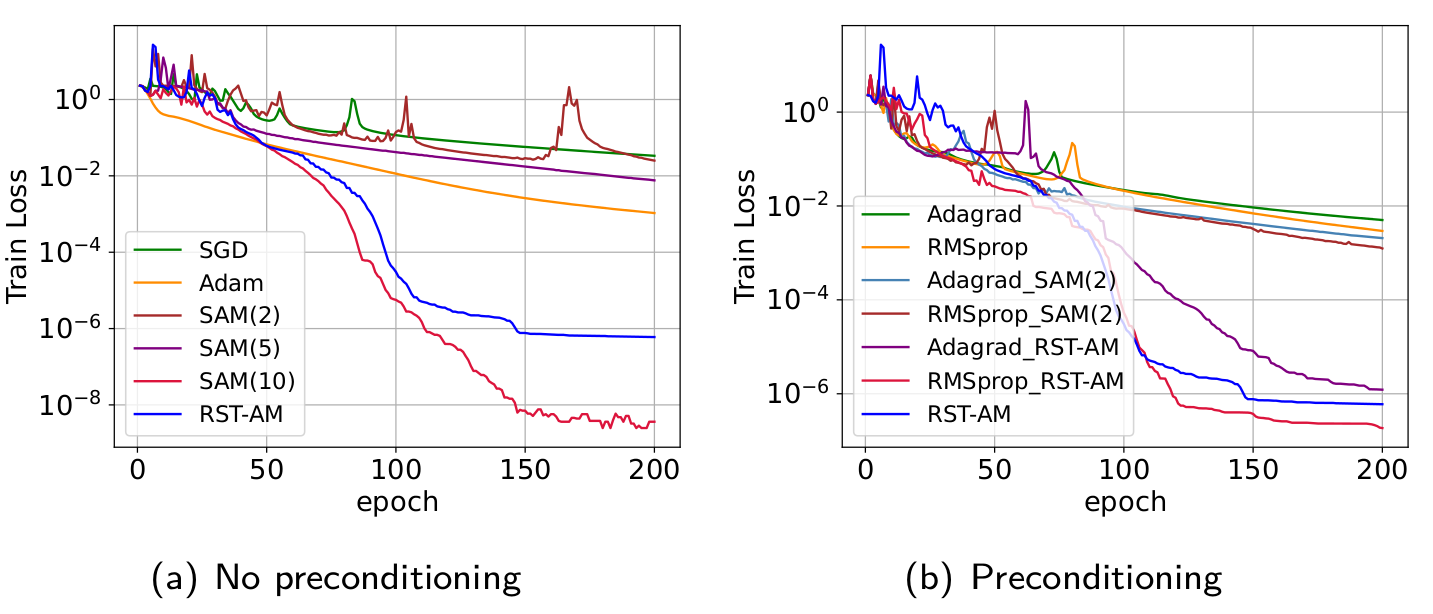
For the full-batch training of a simple convolutional neural network (CNN) on MNIST dataset, the RST-AM can close the gap of the long-memory method (SAM(10)) and the short-memory methods (SAM(2), SAM(5)). The preconditioning is also helpful for the RST-AM.
The experiments of the mini-batch neural networks training include image classification on CIFAR, language model on Penn Treebank, adversarial training, and training a generative adversarial networks.
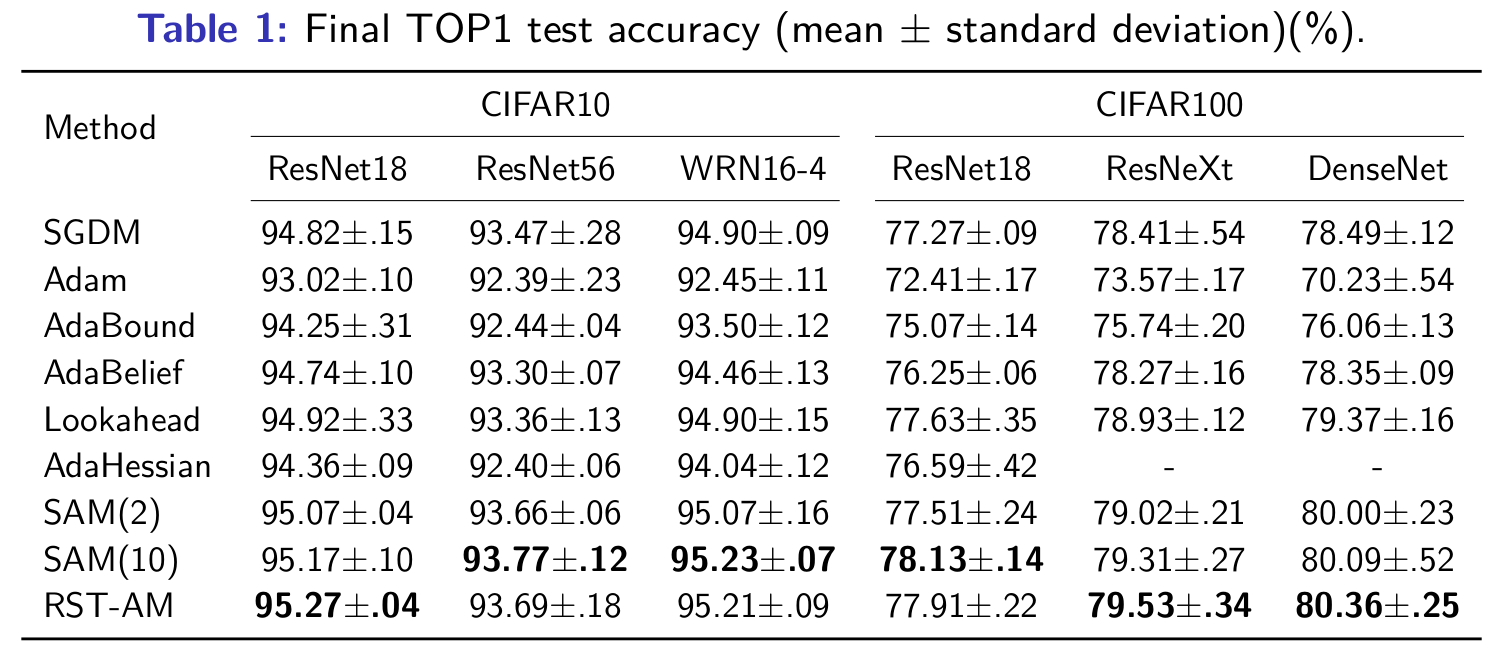

We report the results of the tests on CIFAR here. The numerical results demonstrate that the regularized ST-AM outperforms many existing optimizers while being more memory-efficient than stochastic Anderson mixing. More experimental results can be found in the paper.
Implementation
Here, we give a discussion about the implementation of our methods.

Algorithm 3 describes the details of the RST-AM. When setting \(\delta_k^{(1)} = 0\), \(\delta_k^{(2)} = 0\) and \(\alpha_k = 1\), it is reduced to the ST-AM/MST-AM method. Note that we need to use two matrices \(P, Q \in \mathbb{R}^{d\times 2}\) to store \(P_k\) and \(Q_k\) during the iterations. So this additional memory cost of RST-AM compared with SGD is \(4d\). For the stochastic Anderson mixing, this cost is $2md$, where $m=10$ in the experiments.
The choices of \(\delta_k^{(1)}\) and \(\delta_k^{(2)}\) are
\[\delta_k^{(1)} = \frac{c_1\|r_k\|_2^2}{\|\delta x_{k-1}\|_2^2+\epsilon_0}, \delta_k^{(2)} = \max\{ \frac{c_2\|r_k\|_2^2}{\|p_k\|_2^2+\epsilon_0}, C\beta_k^{-2}\}\]where \(c_1 = 1\), \(c_2 = 1\times 10^{-7}\), \(\epsilon_0 = 1\times 10^{-8}\), and \(C=0\) in our implementation. We found that only \(c_1\) and \(c_2\) need to be carefully tuned in the experiments. Also, the setting that \(c_1 = 1\), \(c_2 = 1\times 10^{-7}\) is quite robust in all of our tests, so this default setting works well. The Line 10 is to guarantee the searching direction is a descent function. In practice, we check \((x_{k+1}-x_k)^\mathrm{T}r_k\) as a simplification. The \(\alpha_k\) and \(\beta_k\) are similar to the learning rate in SGD. Hence, the learning rate schedule directly acts on \(\alpha_k\) and \(\beta_k\).
Conclusion
To address the memory issue of Anderson mixing, we develop a novel class of short-term recurrence Anderson mixing (ST-AM) methods and test it on various applications, including solving linear and nonlinear problems, deterministic and stochastic optimization. We give a complete theoretical analysis of the proposed methods. It is expected that the ST-AM methods can be applied to solve more challenging problems in scientific computing and machine learning, where the high dimensionality prohibits the applications of the classical second-order methods.
Contact
For further discussion, please contact: Fuchao Wei (wfc16@mails.tsinghua.edu.cn).
References
Donald G Anderson. Iterative procedures for nonlinear integral equations. Journal of the ACM (JACM), 12(4):547–560, 1965.
Homer F Walker and Peng Ni. Anderson acceleration for fixed-point iterations. SIAM Journal on Numerical Analysis, 49(4):1715–1735, 2011.
Haw-ren Fang and Yousef Saad. Two classes of multisecant methods for nonlinear acceleration. Numerical Linear Algebra with Applications, 16(3):197–221, 2009.
Alex Toth and CT Kelley. Convergence analysis for Anderson acceleration. SIAM Journal on Numerical Analysis, 53(2):805–819, 2015.
Fuchao Wei, Chenglong Bao, and Yang Liu. Stochastic Anderson mixing for nonconvex stochastic optimization. Advances in Neural Information Processing Systems, 34, 2021.
