Introduction
Chinese word segmentation (CWS) is considered an essential task, which will accurately represent semantic information of Chinese NLP tasks. Recently, good performance for CWS has already been achieved in large-scale annotated corpora as reported by related research. Most methods start with data-driven to improve the performance for CWS, including statistical machine learning methods and neural network methods.
Recent SOTA approaches utilize the pre-trained models (PTM) to improve the quality of CWS. However, the CWS methods based on the PTM only utilize the large-scale annotated data to finetune the parameters. It omits much-generated information of the training step. Besides, the annotated data has some incorrect labels due to lexical diversity in Chinese, therefore the robustness of methods is quite important for the CWS.
In our EMNLP 2021 paper, we propose a self-supervised CWS approach to enhance the performance of CWS model. In addition, we also investigate on the low-quality datasets to analyze the robustness of CWS models. As depicted in the figure below, our model consists of two parts: segmenter and predictor. We leverage the Transformer encoder as a word segmenter. We exploit the revised masked language model (MLM) as a predictor to improve the segmentation model. We generate masked sequences with respect to the segmentation results. Then we exploit MLM to predict the masked part and evaluate the quality of the segmentation based on the quality of the predictions. We leverage an improved version of minimum risk training (MRT) [1] to enhance the segmentation. Experimental results show that our approach outperforms previous methods with different criteria training, and our proposed method also improves the robustness of the model. Our code can be found here.

Methodology
The overall process of our method is shown in the algorithm below. First, we train a word segmentation model and use it to generate segmentation results. Then, according to the segmentation results, the masked sentence is generated based on certain strategies, and an MLM is trained with the masked sentence. Afterward, we mask the sentences in the training set and predict the masked part using the MLM to evaluate the quality of the segmentation results. Finally, we use the results to aid the training of the segmentation model.

Segmentation Model
The model architecture is shown in the figure below. Our segmentation model architecture is based on BERT [2]. The input is a sentence with character-based tokenization and the output is generated by a BERT model and a CRF layer sequentially. The segmentation results are represented by four tags B, M, E, and S. B and E denote the beginning and end of a multi-character word, respectively. M denotes the middle part of a multi-character word, and S represents a single-character word. Our segmentation model is initialized with PTM (i.e. BERT) and trained with negative log-likelihood (NLL) loss.

Revised MLM as Predictor
In this work, we use a revised MLM similar to BERT [2] to evaluate the quality of segmentations. However, the masking strategy adopted in the training of the Chinese BERT PTM makes the character a unit. This masking strategy cannot reflect the segmentation information, thus we design a new masking strategy that can reflect the segmentation information:
- Only one character or multiple consecutive characters within a word can be masked simultaneously.
- We set a threshold \(mask\_count\). If the length of a word is less than or equal to \(mask\_count\), the entire word will be masked. Otherwise, we randomly choose consecutive \(mask\_count\) words and mask them.
- From all possible maskings, we randomly select one with equal probability and apply it to the input.
An example of the masking strategy we introduce above is shown in the table below.
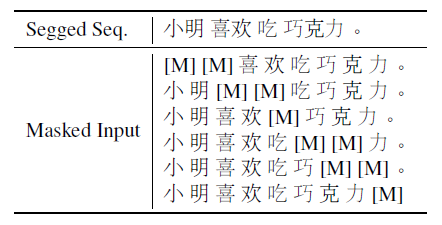
When evaluating the quality of segmentation results, we first find all the legal masked sequences based on the segmentation result. Then, we use the revised MLM to evaluate the prediction quality of all masked words in these inputs. We take the average of all the quality scores as the quality of the segmentation result:
\[\begin{equation} q(\mathbf{y}, \mathbf{x})=\mathbf{E}_{\mathbf{x}_m|\mathbf{x}_o^{(s)},y;\gamma}\left[\Delta\left(\mathbf{x}_m, \mathbf{x}_m^{(s)}\right)\right]=\sum_{\mathbf{x}_o^{(s)}{\in}M(\mathbf{x},\mathbf{y})}P(\mathbf{x}_m|\mathbf{x}_o^{(s)};\gamma)\Delta\left(\mathbf{x}_m, \mathbf{x}_m^{(s)}\right), \end{equation}\]where \(\Delta\left(\mathbf{x}_m, \mathbf{x}_m^{(s)}\right)\) denote the difference between the prediction results of the masked part \(\mathbf{x}_m\) and the ground-truth of the masked part \(\mathbf{x}_m^{(s)}\), which can be obtained from BERT embeddings.
Training Procedure with Improved MRT
After we train the segmentation model with NLL loss, we further train it using MRT [1]. Specifically, on the training data \(\mathbf{X}\), we optimize
\[\begin{equation} J(\theta){\approx}\sum_{\mathbf{x}{\in}\mathbf{x}}\mathbf{E}_{\mathbf{y}|\mathbf{x};\theta,\alpha}\left[q(\mathbf{y}, \mathbf{x})\right]=\sum_{\mathbf{x}{\in}\mathbf{x}}\sum_{\mathbf{y}{\in}S(\mathbf{x})}Q(\mathbf{y}|\mathbf{x};\theta,\alpha)q(\mathbf{y}, \mathbf{x}), \end{equation}\]where \(Q(\mathbf{y}\mid\mathbf{x};\theta,\alpha)\) is a distribution defined on a subset \(S(\mathbf{x})\) of the segmentation results:
\[\begin{equation} Q(\mathbf{y}|\mathbf{x};\theta,\alpha)=\frac{P(\mathbf{y}|\mathbf{x};\theta)^{\alpha}}{\sum_{\mathbf{y}'{\in}S(\mathbf{x})}P(\mathbf{y}'|\mathbf{x};\theta)^{\alpha}}. \end{equation}\]However, the MRT loss can only provide a weak supervision signal, because when the denominator of \(Q(\mathbf{y}\mid\mathbf{x};\theta,\alpha)\) becomes smaller, the loss can be rather low even if the value of \(P(\mathbf{y}\mid\mathbf{x};\theta)\) is very small (see the table below).
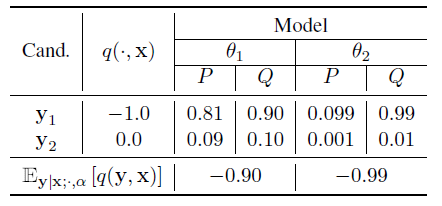
This may decrease the probability of some good segmentation results, thereby reducing the performance of the segmentation model. Therefore, we modify the MRT loss by adding a regularization term to mitigate the impact of getting the denominator of \(Q(\mathbf{y}\mid\mathbf{x};\theta,\alpha)\) smaller:
\[\begin{equation} J(\theta)=\sum_{\mathbf{x}{\in}\mathbf{x}}\bigg(\sum_{\mathbf{y}{\in}S(\mathbf{x})}Q(\mathbf{y}|\mathbf{x};\theta,\alpha)q(\mathbf{y}, \mathbf{x})-{\lambda}{\sum_{\mathbf{y}'{\in}S(\mathbf{x})}P(\mathbf{y}'|\mathbf{x};\theta)^{\alpha}}\bigg). \end{equation}\]Results
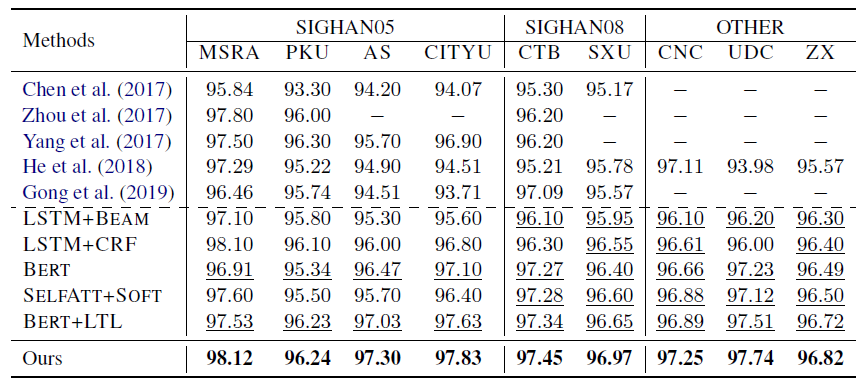
To investigate the quality of our segmentation model, we compare our approach with the previous SOTA methods on the 9 benchmark datasets of CWS. As shown in the table below, our proposed method obtains better results on different standard datasets with single criterion learning.
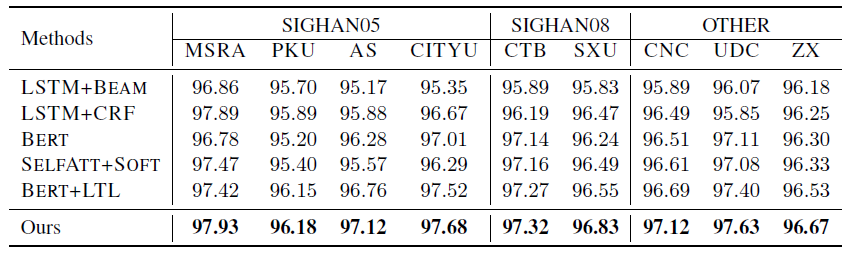
To analyze the robustness of our proposed method with respect to the revised MLM, we prepare noisy-labeled datasets which contain 90% real data and 10% randomly shuffled data. As shown in the table below, all the results are almost lower than the results from single criterion training. However, our proposed method still gains better results than SOTA baselines with noisy-labeled datasets rather than the standard labeled data.
More results can be also found in our paper.
Conclusion and Future Work
In this work, we propose a self-supervised method for CWS. We first generate masked sequences based on the segmentation results and then use revised MLM to evaluate the quality of segmentation and enhance the segmentation by improved MRT. Experimental results show that our approach outperforms previous methods on both popular and cross-domain CWS datasets, and has better robustness on noised-labeled data. In the future, we can also extend our work to tasks of morphological word segmentation (e.g., morphological analysis). For further discussion, please contact: Mieradilijiang Maimaiti (miradel_51@hotmail.com).
References
[1] Shiqi Shen, Yong Cheng, Zhongjun He, Wei He, Hua Wu, Maosong Sun, and Yang Liu. 2016. Minimum risk training for neural machine translation. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics, ACL 2016, August 7-12, 2016, Berlin, Germany, Volume 1: Long Papers. The Association for Computer Linguistics.
[2] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, June 2-7, 2019, Volume 1 (Long and Short Papers), pages 4171–4186. Association for Computational Linguistics.
